Motivation
This posts takes the (Leetcode 1) classical two sum problem and solves it using two pointers. However post takes the excellent formal and informal solution from this stackoverflow post and elaborates on the nuances and interesting observations.
Seeing as though there are other problems that follow the same pattern I think it helps really breaking down the intuition between when you can re-use this intuition. Note that although this problem is tagged as an “easy” problem, the solution that we’re looking at is similar to the medium level problem Leetcode 11: Container with Most Water
This post will best be appreciated by
- Attempting the problem
- Sleeping on it
- Reading the solution
- Reading the Stack Overflow post
- Sleeping on it
Intuition: Why start at the first and last elements?
It did not seem like it at first but there is a surprising amount of detail as to why we start the pointers at the first and last elements. Due to the nature of a sorted array you end up with this unique property.
The sum of the two numbers at these pointers (the sum of the first and last elements) will initially give the largest possible sum for the first pointer and smallest possible sum for the second pointer.
Why does this matter? The key is really understanding that the solution is looking for a pair of indices. With this unique property we can actually safely and systematically eliminate an index from the solution at each iteration. The solution described in the more formal solution of the SO post highlights this as well. It points out that what we’re really out to prove is that while we iterate through the array using the two pointers we properly eliminate an index from the solution.
Roughly speaking this means we start with a potential solution (l, r) where l is the index of the first element and j is the index of the last element.
If we calculate the sum of the two numbers and we get a value larger than the target sum, we can safely eliminate the index r (the largest number) from the solution. Remember that the unique property is that for the leftmost index we’re looking at the largest sum and for the rightmost index we’re looking at the smallest sum.
Let’s look at an example to see why this is true.
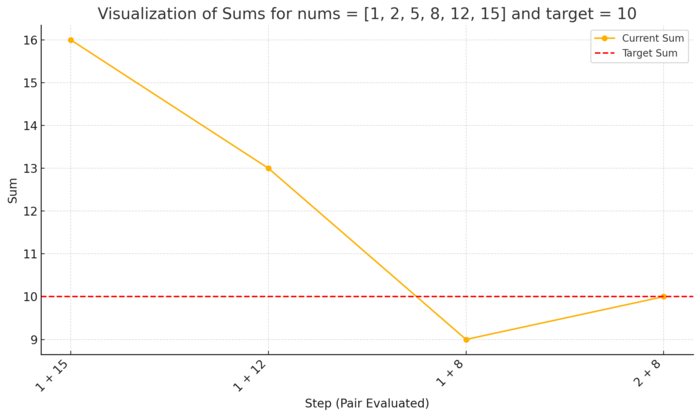
nums = [1, 2, 5, 8, 12, 15]
target = 10
# will get smaller and smaller
sum(0,5) = 1 + 15 = 16
sum(0,4) = 1 + 12 = 13
# gets larger and larger
sum(1,5) = 2 + 15 = 18
sum(2,5) = 5 + 15 = 20
The sum in this case is 16 which is larger than the target sum of 10. Remember that for the rightmost index we’re looking at the smallest sum. So now we know that we need a smaller sum yet that’s not possible with this pair.
Furthermore, we can safely remove the index r from the solution. This is because we know that there is no what to keep the rightmost index of the solution while decreasing the sum of the two numbers since with the right index fixed on 5, any other index would give an even larger sum.
On the next iteration we’ll have a similar case where the sum is greater than the target sum. For additional reassurance, let’s imagine keeping the right index fixed on 4 and see what happens.
nums = [1, 2, 5, 8, 12, 15]
target = 10
sum(0,5) = 1 + 15 = 16
sum(0,4) = 1 + 12 = 13
# gets larger and larger
sum(1,4) = 2 + 12 = 14
sum(2,4) = 5 + 12 = 17
As we can see the sum only got larger and therefore again we can safely eliminate the index r from the solution.
Finally let’s look at the case where the sum we get is smaller than the target sum.
This is when l = 0 and r = 3 where the target sum is 10 but the current sum we
get is 9.
Similarly in this case we can safely remove the leftmost index as a viable pair in the solution. This is because the sum for the leftmost index is the largest it can be. So in the situation where we want to get a larger sum, it’s just not possible.
nums = [1, 2, 5, 8, 12, 15]
target = 10
# keeping the leftmost index fixed on 0
sum(0,3) = 1 + 8 = 9
sum(0,2) = 1 + 5 = 6
Touch of Formality
To make things a little more formal, and to draw back to the Stack Overflow post, we’re picking a pair of indices (l, r) where l starts as the index of the first element and r is the index of the last element. On each iteration we’re assuring that we’re only safely eliminating an index that is impossible to be in the solution. Since we’re guaranteed that the target sum is possible we’re sure that we’ll eventually get to a solution.
Conclusion
With ordered arrays and the two pointer solution the goal is usually to find some “direction” we can go that still guarantees that we’re able to find a solution. In these types of problems it’s a little weird at first since we’re not looking at the sums being ordered.
If we move the rightmost index to the left then the sum gets larger but if we kept the rightmost index and moved the leftmost index to the right then the sum gets smaller.
The key is realizing
- for the rightmost index we’re looking at the smallest sum
- for the leftmost index we’re looking at the largest sum
This gives us a way to navigate towards the array. We have found how to navigate through the array but this way is unique since we essentially have two anchors. This also explains how we can navigate through this array where the sum is not monotonic.