Peak and Valley View (Which history you want determines which form of monotonic stack/queue to use)

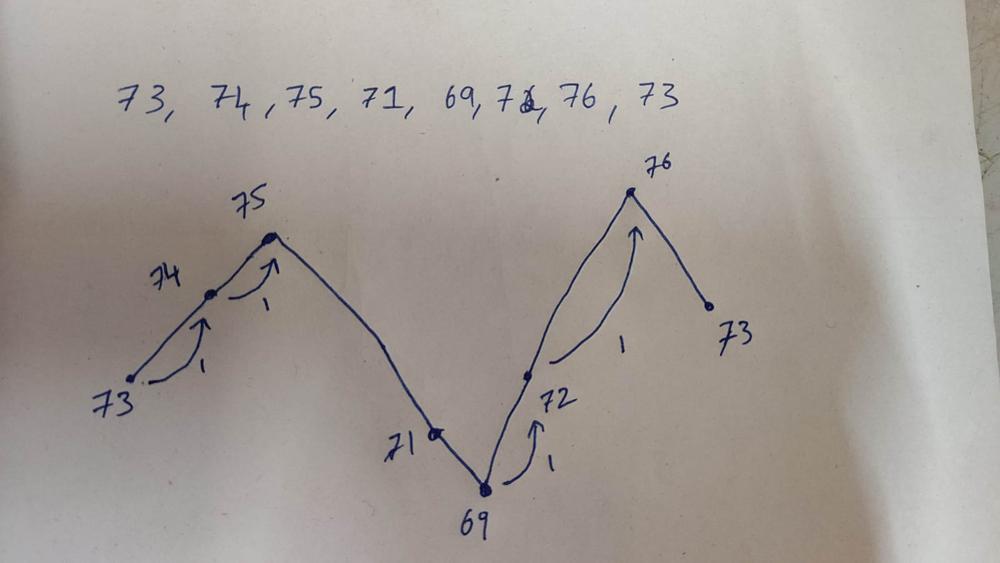
1. First Uphill: Until we reach a peak we know that the values must be increasing. Therefore, for all the values until the peek, every temp next to it is greater than previous. 73 < 74 < 75
2. Downhill: Until we reach the valley we know that the values are decreasing. Since we’re looking for the next greater elements in this case these values have to wait for the next peak.
   • Think of one of the values on this downhill. For example, 71 needs to wait until we start climbing uphill in order to find an element greater than it.
3. Nth Uphill: Once increasing values found, look back all the elements in valley(this means elements from the most recent peak to most recent valley) lesser than the increasing value.
   • Now that we’re increasing again we can take a look at the elements that were waiting for an increasing value.
   • 72 finds [75, 71, 69] in the stack. We see that 72 > 69 and 72 > 71 so we’ve found the next greater element. Stack is now [75]
   • 76 finds [75] in the stack. 76 > 75 so we’ve found 75’s next greater element. Stack is now []

In this problem we’d want a monotonic decreasing stack. The reason behind this is because of the key insight of 2. While we’re waiting for the second uphill this is where we want to collect the list of elements waiting for an increasing value.

We collect [75, 71, 69] with 69 being the top of the stack. The incoming element is 72 which we can see will be greater than 69 and 71. This means that we have found the next greater element for both 69 and 71 but not yet for 75. On the next iteration we have [75] left on the stack and the incoming element is 76. This allows us to pop of 75 as well since we’ve found the element after 75 that has a greater value.

Random observations

• We know for sure that the value on the uphill right after the peak must be greater than the peak

Breaking down intuition

Visualize the array as a line graph, with (local) minima as valleys. Each value is relevant for a range that extends from just after the previous smaller value (if any) to just before the next smaller value (if any). (Even a value larger than its neighbors matters when considering the singleton subarray that contains it.)

In my head this represents that if you look at 74 on the line graph the previous smaller value is 73 which is just next to it. Howver the next smaller value is 71.

Recognizing that a value shadows every value larger than it in each direction separately This means that every smaller value behaves as the shadow of every larger value. For example, 71 shadows the 76 ahead of it and the 75 behind it.

… , the stack maintains a list of previous, unshadowed minima

An unshadowed minima is a value that itself does not shadow any value which is the same as saying this value has nothing smaller than it.

This makes sense since the stack is a monotinicly increasing in this case. So as you’re iterating through t

[the] stack maintains a list of previous, unshadowed minima for two purposes: identifying how far back a new small number’s range extends and (at the same time) how far forward the invalidated minima’s ranges extend.

Ephasizing on both directions

73, 74, 75, 71, 69, 72, 76, 73 The monotonic stack can help you determine the next largest or smallest going in both directions. Let’s focus on picking the next largest element. So if we pick 69 we see that if we move to the left the next largest is 75. The next largest going to the right would be 72.

Decreasing Monotonic Stack

Downhill: [75, 71, 69] If you take an element and look to its left you can find the previous elements that are greater. 71 is the first greater element going to the left. Looking in the input array we see that 72 is the next greater element going to the right.

• You can’t use it to find all the elements greater to the left.
  • 73 and 74 are also greater than 69 but they were popped off earlier
• You can’t use it to find all the elements greater to the right
  • As soon as you see a larger element 69 gets popped off the stack so we’ll lose info

When you pop an element because we’ve found a larger element, the element that causes us to pop is the next largest value going to the right of the element.

• 72 causes 69 to pop. 72 is the next greater element of 69 going to the right. The value of the element below in the stack is the next larger element moving to the left.
• When 69 enters we have 71 already there. 71 is the next larger element going to the left

Resources

https://leetcode.com/problems/daily-temperatures/solutions/2924758/efficient-and-simple-intution-solution-with-o-n-space-and-time-peek-valley-approach/
https://brilliantprogrammer.com/blog/what-is-monotonic-stack/ best short and sweet
https://stackoverflow.com/questions/55780200/intuition-behind-using-a-monotonic-stack good intuitive answer
https://leetcode.com/problems/daily-temperatures/solutions/1682915/illustrated-explanation/ good image
https://medium.com/techtofreedom/algorithms-for-interview-2-monotonic-stack-462251689da8 introduces idea of range queries
https://leetcode.com/problems/sum-of-subarray-minimums/solutions/2118729/very-detailed-stack-explanation-o-n-images-comments/?orderBy=most_votes great answer to similar problwem\

One

https://1e9.medium.com/monotonic-queue-notes-980a019d5793 good interactive ui