Introduction

After some time working on Leetcode you start to realize trends in the problem. One category that I have recognized is one where the “elegant” solution uses simple logic to narrow out work.

Brute Force

Create a sliding window with the size of minSize. One of the rules that we need to follow is that the number of unique characters < maxLetters. This is easier than you might think. We can keep track of frequencies with a map. This allows us to tell apart similar words like aab and aba. aab -> {a:2, b:1} aba -> {a:1, b:2}

How do we determine if the unique characters < maxLetters? In python we can just check the length of the keys of the dictionary. In python it’ll easily count the number of keys with the len function. aab -> {a:2, b:1} -> len(dict) = 2 aba -> {a:1, b:2} -> len(dict) = 2.

Now we wrap all this work into another loop since we’d need to repeat the process for all sliding window lengths from [minSize, maxSize] inclusive.

Unique vs Distinct

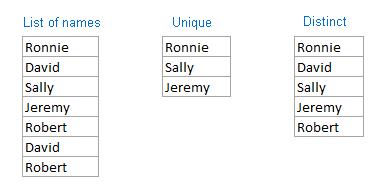
There is a slight distinction in these two similar sounding words that someone in the comments pointed out. This basically says that the problem statement had an ambiguity. If you think of them as the functions given a list of values UNIQUE(list) will return the elements that only appear once. DISTINCT on the other hands returns all the different values found in the list. It will only return one instance of each value.

I think these tables found on an Excel blog put it into perspective.

Realization that maxSize is redundant

ababab, maxLetters 2, minSize = 2, maxSize = 4 If we start out with maxSize we find that abab has two occurances. However it is actually always better to start with the minSize. ab is also valid and if you notice it occurs 3 times.

Let’s say we have a string with size X and substring with size Y. Both these lengths are within the allowable range (minSize and maxSize). If string X is a valid string (its unique characters < maxLetters) then string Y is also valid since it will contain less than or equal to string X’s unique characters. In this problem the smaller size valid occurances are optimal. A larger string can be broken up into multiple valid occurances of smaller strings.

Python code tips

In my code I created the window size then started another loop where the core logic is.

for right in range(minSize - 1,len(string)):

My reasoning was that if we have a window with size 3, we want to iterate from index 2 until the len(string)

Another approach would be to start from the beginning and go until the window We know that we want the window size to be minSize so we can just iterate from 0 to len(s) - minSize. For example minSize = 3 len(string) = 5 aabaa The valid window sizes are [0,2], [1,3], [2,4] which relate to aab, aba, baa So we just want to iterate from 0 -> 2. The window is from index + windowSize

for i in range(len(s) - minSize + 1):

Takeaway

Always think critically. Well no duh. But once you think you have a correct way to handle the brute force method see if there are observations you could make with the problem. Just think very broadly and ask yourself questions about the nature of the problem.

Links

https://leetcode.com/problems/maximum-number-of-occurrences-of-a-substring/solutions/734807/Hint:-maxSize-doesn't-matter!/ If you are able to find substrings with size > minSize meeting the maxLetters reqirement, substrings with smaller sizes have atleast the same frequency!

https://leetcode.com/problems/maximum-number-of-occurrences-of-a-substring/solutions/888643/java-easy-to-understand-solution-o-n/?orderBy=most_votes The reason is that for example “aababcaab” maxLetter = 2, minSize = 3, maxSize = 4 Once we found “aa” occur twice we know anything longer cannot occur more than that. Therefore the substring length construct with minSize is always >= substring length construct with maxSize.

In a comment @jiansun518 for example Let the minSize be 2. if you found “abc” occur twice in “abcabc”. As “ab” is part of “abc”, then its implied that you will find “ab” or “bc”(substrings of “abc”) twice in “abcabc”

Code

Brute Force

def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:
    N = len(s)
    left, right = 0,0

    occurances = defaultdict(int)
    for size in range(minSize, maxSize + 1):
    window = defaultdict(int)
    for i in range(size-1):
        char = s[i]
        window[char] += 1
        right += 1

        for right in range(right,N):
            char = s[right]
            window[char] += 1


            if len(window) <= maxLetters:
            occurances[s[left:right+1]] += 1

            char_to_remove = s[left]
            window[char_to_remove] -= 1
            if window[char_to_remove] == 0:
            del window[char_to_remove]
            left += 1

    item = 0
    for string, count in occurances.items():
        item = max(item, count)

    return item