Characteristics of the problem
- You can’t start out with the root (lowest common ancestor)
- This is really a traversal problem
- Each node has a range of values that it could contain which is from [min(leftSubtree), max(rightSubtree)].
- Understanding this range means we know the possible children of a node through its value.
We’ll explore the last two towards the end of the blog since these are not as intuitive.
You can’t start out with the root
In the constraints of the problem we have the added information that the nodes that we’re interested (p and q) are guaranteed to be in the tree. If we try a solution with the root as a candidate it is guaranteed to be an ancestor! However, it will not be the lowest common ancestor.
Gaining Observations through examples
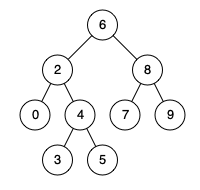
Example 1 (p = 2, q = 8)
It ends up being that the root is the lowest common ancestor. In this case the lowest common ancestor has found p in in the left subtree and 8 in the right subtree
Example 2 (p = 0, q = 5)
We start at the root and see that the nodes we’re interested in are not in the right subtree so we can ignore it. We’ll just travel left. We see that the left node finds one of the nodes we’re interested so that’s good.
- Can we stop exploring subtree if you find value?
Example 3 (p = 4, q = 5)
One question that came up for me is can you stop exploring a subtree if one of the nodes was found. Let’s take this case as an example. We start at the root node and notice that the right subtree doesn’t contain p or q. Therefore our LCA must be in the left subtree. Looking at node 2, we notice that neither p or q are in the left subtree. Our LCA must be in the right subtree. It was not enough that the node 2 found p. We can see q is in the right subtree of node 2 however the reason it does not matter is because 4 counts as a decendant of itself. This was allowed in the problem statement.
we allow a node to be a descendant of itself
If it’s a single subtree then the case is actually simple just return the first node we find. In example 3, we can immediately stop as soon as we find that the node we’re looking for. Remember that we’ve explored node two and saw that
- 2 != p or q (2 != 4 or 2 != 5)
- We also saw that at node 2, it’s left subtree doesn’t contain 4 or 5.
This means that 4 and 5 which we know exists due to the constraint of the question must be in the right subtree. The fact that the left subtree of 2 did not find p or q is important. Since if node 2 did find p or q in its subtree then it would be the LCA. However, since it did not find it and then we immediately find it in one of the nodes we’re interested in, in node 4 we can stop searching.
Observation

The LCA will have its decendants in
- Both subtrees
- A single subtree (Example 3)
Using the BST to our advantage
In both previoius solutions we’re needlessly exploring the whole tree. In the leetcode solution provided they also did not take advantage of the fact that the problem was specifically for Binary Search Trees
As this is BST, as soon as we discover that one value is less (on the left) and another one is more(on the right) than the current node we can say that this is the LCA, without even going through whole tree traversal.
This flips the question into thinking about it as travel to the point in the tree where smallerNode <= node <= largerNode where smallerNode = min(p,q) and largerNode = max(p,q)
The algorithm becomes:
-
min_val <= node.val <= max_val
- It means min_val is inside the left subtree and max_val is inside the right subtree -> The LCA is the node
-
min_val < max_val < node.val
- It means min_val and max_val are inside the left subtree -> The LCA is inside the left subtree
-
node.val > max_val > min_val
- It means min_val and max_val are inside the right subtree -> The LCA is inside the right subtree
Proving why this is just a traversal problem
Even when I understood the fact that a LCA ends up being the point where we find a split in the tree I didn’t understand how this changes into becoming a search for the first node within the range of [smallerNode, largerNode]. The reason why is because the Binary Search Tree is a specific tree. A split will only occur when we are at a node that has smaller values and larger values. We’re looking for specifically the point at which smallerNode and largerNode split off at.
Let’s say we’re at a node where min_val <= node.val <= max_val.
Proving that it must be the first node that satisfies min_val <= node.val <= max_val.
Why does it have to be the first node that satisfies the condition? Can we have another node that satisfies the same condition be the lower common ancestor?

That would be like finding [0,9] If we see start at the root it has a value that satisfies the condition and we can see that the root is the LCA. Let’s see if we can go to one of the children node and see if that could be the LCA. If we travel to the left node we see that the condition is still true. 0 <= 2 <= 9 however at this point we see that the 9 node is not a decendant of node 2. If we travel to the right node we see that the condition is still true. 0 <= 8 <= 9 however at this point we see that the 2 node is not a decendant of node 8.
It must be the first node we find that satisfies the constraint
Example 3 Revisited (p = 4, q = 5)
We start at the root which has a value of 6.
- 6 is greater than the maxNode so that means that the current root is not a LCA. We need to find a smaller node that is within the range of [4,5]. A smaller node exists in the left subtree since it’s a BST. Go to the left subtree
- 2 is now too small so the current root is not a LCA. We need to find a larger node that is within the range of [4,5]. A smaller node exists in the left subtree since it’s a BST. Go to the left subtree
- Now that we reached 4 we can just return since we found the LCA
Recap / Crutial Observations (Each BST node has a range)
Somewhat surprisingly this is just a traversal problem. A node with value X in a BST can have a subtree where the left subtree can contain any value < X and a right subtree where it can contain any value > X. Assuming we’re just looking a BST that won’t be modified, a node of that BST can contain all elements [min(leftSubtree), max(rightSubtree)]. In this problem we specifically want the element that contains the [smallerNode, largerNode] range.

- The relationship is that based off the node’s value in a BST we know its possible decendants.
- Any node in a BST can contain min(leftSubtree), max(rightSubtree)
- Example: Node 2 can contain [0,5]
- We’re also told that the decendants must exist in the problem constraints. So if we find a node where its value is within the [smallerNode, largerNode] constraint, then we know that we’ve found the LCA
- If we’re looking for smallerNode = 3 and largerNode = 5
So we can think of each node having a range. Each node has a range of values that it could contain which is from [min(leftSubtree), max(rightSubtree)]. Understanding this range means we know the children a node could contain given its range. For example if range of Node 2 is [3,5] and we know that a node with value 3 and 5 exist then it must be a child of Node 2.
Each Node’s range is unique. If we know a node’s range is [A,B] then the left child and right child of the node would have a different [min(leftSubtree), max(rightSubtree)]
Further Reading
Naive Brute Force Recusive Solution
https://stackoverflow.com/a/75379001/8262460
At a high level the simplest thing you can do is traverse the entire tree, keep track of your path until you reach p and q.
In Example 2,
the path to node 0 is [6,2,0] the path to node 5 is [6,2,4,5]
Since we’re looking for the lowest common ancestor we just need to iterate in reverse. Otherwise the root node would always be returned since it’s always a LCA.
for node in [0,2,6]:
if node in [5,4,2,6]:
return Node
Backtracking Solution
Intuitively this was the first thing that popped out to me. It’s a tree problem so recursion is probably fair game. It involves more decision making than typical recursion so backtracking comes to mind in those cases. This form of solution is also not that hard to think out. Given that we attempt the solution after we realize that we need to start
If a node is the common ancestor then the children nodes can be found: 1. In the left subtree AND right subtree 2. Just in the left subtree 3. Just in the right subtree
Resources
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/solutions/2413331/python-easiest-solution-detailed-graph-explantion-dfs-beginner-friendly/?orderBy=most_votes
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/solutions/2414941/python-detailed-explanation-easily-understood-o-h-o-n/
https://stackoverflow.com/a/75379001/8262460\