Introduction

I found a few resources that I think did a decent job at explaining bits and pieces but not the full thing. This is also a tool for me to think things through as I go through the proof.

Leetcode solution with useful insights
Math stackexchange with useful insights
Neetcode’s solution, useful insights on proof
Unrelated but cool modulus related history

Note for clarity

First node of the tail means -T First node of the cycle means 0

In the cycle scenario

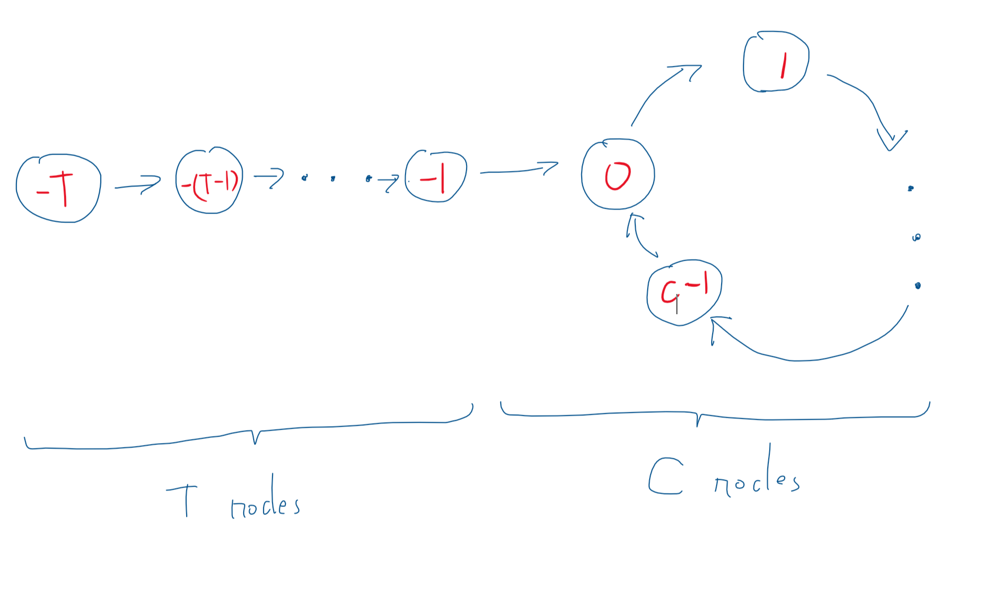T represents the tail. I believe it is called tail because it looks like the tail of a tadpole.
C represents the Cycle

Let’s say the tortoise takes T steps from the start. This means the tortoise is now on node 0 (the start of the cycle). Using the fact that we know the hare takes two steps for every step the tortoise takes we know the hare has travelled 2T. Where is the hare though? We can make another observation that the hare is currently stuck inside the cycle. This is because we know a cycle exists (our assumption in the beginning of the problem), if the slower moving tortoise made it to the start of the cycle then the faster moving hare must already be there. Let’s call the node that the hare is on at the time of the tortoise entering to be called r.

If the hare has travelled a distance of T after it entered the cycle we can determine a few more things. We know that we travelled T distance while inside the cycle, we know that the cycle has a total of C nodes. There must be a relationship between C and T then. Let’s think of an example to see if we can come up with it.

• If C = T then this means the hare would end up at the start of the loop at the same time the tortoise does. r in this case would be Node 0.
• For same reason as above this means that if T is some multiple of C then r = 0. (T = kC)
• If T = 12 and C = 5. This means the hare travelled 2T or 24 nodes. Starting from the first node of the tail (-1) we move 12 nodes and now we’re at the start of the cycle. We need to move 12 more so where do we land. We go around the cycle twice which means we’ve went a total of 10 more nodes. 12 + 10 = 22. We need to travel 2 more nodes. r = 2

Math!

Suprise we’re using modulus. This is one of the few times were modulus was in directly in the nature of the question and not just an operation to perform. In the most recent example it’s a little more clear if you look at it. Phrasing it in a more obvious way when the hare gets to the start of the cycle it has 12 more nodes to travel. The length of the cycle is 5 nodes. 12 % 5 = 2. Another surprise is why the articles called the node hare lands on as r. It’s just short for remainder.

Understanding C - r relationship

If the hare is at a node in the cycle labeled r and the tortoise is at the start of the cycle, then the distance between the two is C - r. Let’s say that r is node 1 in the picture. Even though the tortoise looks close to the hare in this picture the direction of the cycle matters. The hare can only move forward so the only way it can catch up to the tortoise is by overlapping it. It must travel more than one cycle to catch up to it.

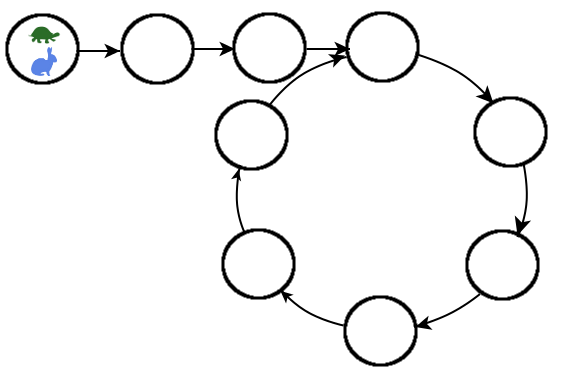
Let’s look at a more specific image. If the hare is on the node right after the start and the tortoise is on the start, the distance between the two is really 6 - 1(C = 6, r = 1). They are 5 nodes apart.

Once they’re both in the cycle, it will take C - r steps to meet

The Neetcode youtube video shows this well. To summarize this part once they’re both in the cycle we know how each one moves. Tortoise gets one step farther but hare will get two steps closer. When the tortoise gets farther the distance grows from C - r -> C - r + 1. However, the hare will take two steps forward. C - r + 1 -> C - r - 1. The distance decreases by 1. Now it’s just a simple coding loop decrementing by 1. Eventually it will be 0.

This proves:

1. If a loop exists that the hare will catch up to the tortoise
2. If a loop exists, once the tortoise enters the cycle. It will take extactly C - r steps for the hare to catch it.

Proof it’s O(n) time complexity

The leetcode link makes a good point. At first glance it’s not obvious that the algorithm has a O(n) time complexity.

If a cycle exists, couldn’t we loop so many times where the algorithm is not O(n) it would be more like O(5n)

Our math to determine that after the tortoise takes T steps, it will be caught in C - r steps helps us answer the point above. T < number of total nodes. C - rem < the total nodes. remainder is also guaranteed to be < C since it’s a remainder. Therefore since T and C - rem are both less than total number of nodes we can safely say our time complexity is O(n).